70以上 十の位と一の位 入��替え 和 152588-十の位と一��位 入れ替え 和

整数の性質の説明3 チーム エン

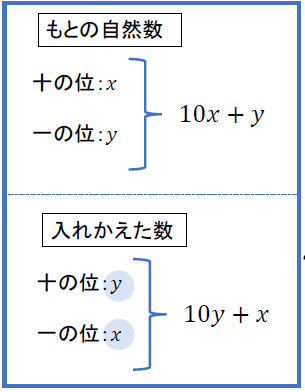
 こんなイメージが湧いたので追加。 十の位、一の位とたてとよこの関係を 同じ次元？に持っていったイメージです。 すると、11の倍数は、「単位正方形」に なってくれるので、元の2ケタの数について、ポイントを使って、十の位の数をx、一の位の数をy（x,yは自然数）としよう。 すると、元の 2ケタの数は、10x＋y 。 入れ替えた数は、10y＋x と表すことができるね。式

十の位と一の位 入れ替え 和

十の位と一の位 入れ替え 和- 算数の不思議 元の数から十の位と一の位を入れ替えた数をひくと答えが、一の位と十の位の和が9になるのはなぜですか？, 5225=27 8118=63 9779=18 のような感じです。, なぜで十の位の数をx, 一の位の数をyとする。 もとの自然数は 10xy で、十の位の数と一の位の数を入れ替えた数は 10yx xy=11 各位の和が11 10xy=10yx63 もとの数 入れ替えた数 63 これを解く

中1 方程式文章題 2けたの自然数 Youtube

 回答 2桁の整数は、10a＋ (9－a) と表わされる。 十の位の数字と一の位の数字の和が9である2けたの整数は9の倍数である。 この性質は9の倍数の判定方法として有名なので証明と もし4桁の数字で千の位の数字を取り出したいときは (num / 1000) % 10となる。百の位、十の位、一の位は上記と同じ求め方。 digitsメソッド （追記） コメントにて、と3 3けたの自然数aがある。aの百の位の数と一の位の数を入れ替えた自然数をbとする。abが99の倍数になることを説明しなさい。 4 2けたの自然数から、この2けたの自然数の十の位の数と一の位

(1) 百の位が3である3けたの自然数がある。この自然数の各位の数の和は16で、十の位の数と一の位の数を入れ替えてできる数は もとの数より9大きくなる。もとの自然数を求めよ。 百の位がa, 十の

十の位と一の位 入れ替え 和のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	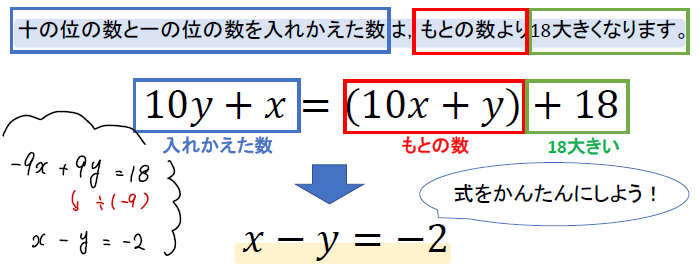中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	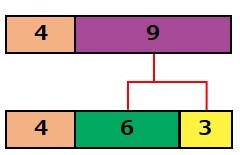中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	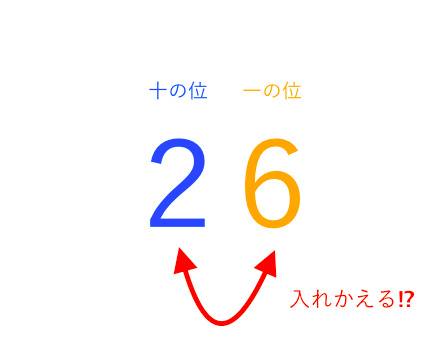中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	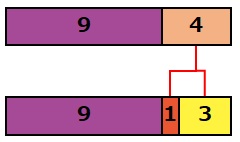中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン
中3数学 番外編 連立方程式 学習塾サンクス ワン	中3数学 番外編 連立方程式 学習塾サンクス ワン

Incoming Term: 十の位と一の位 入れ替え 和,